背景

最近无意间看到一个初中的奥数题, 题目是: , 求x 的值是多少？

解题过程

• 要解决方程 ，我们首先要理解这是一个无穷递归幂塔。我们可以将其表示为一个固定点问题。设

• 根据题意，我们有：

• 从而：

其他参考的通用解题方法

方法一：固定点法(解题过程的方法)

假设 ，则 满足：

本文介绍几何图形的面积周长公式汇总

正方形（Square）

• 周长（Perimeter）:
• 面积（Area）:

长方形（Rectangle）

• 周长（Perimeter）:
• 面积（Area）:

圆形（Circle）

• 周长（Perimeter）:
• 面积（Area）:

本文介绍基础数学公式

1. 毕达哥拉斯定理 (Pythagoras, 530 BC)

简要说明：在直角三角形中，直角边的平方和等于斜边的平方。这是几何学的基础。
作者介绍：毕达哥拉斯是古希腊数学家和哲学家，被誉为“数学之父”。

2. 对数 (John Napier, 1610)

简要说明：对数的乘法法则，两个数的对数之和等于这两个数相乘的对数。
作者介绍：约翰·纳皮尔是苏格兰数学家，以发明对数和纳皮尔计算尺著称。

本文介绍高等数学中的leaky ReLU，以及在神经网络中的应用。

函数原型

leaky ReLU（带泄露的ReLU）

其中为泄露率，取

导数的函数原型

适用范围

默认全部

函数图像

本文介绍高等数学中的ReLU，以及在神经网络中的应用。

函数原型

ReLU(Rectified Linear Unit 修正的线性单元)

导数的函数原型

适用范围

二分类问题选择sigmoid，余下的问题ReLU是默认的选择

函数图像

本文介绍高等数学中的sigmoid函数，以及在神经网络中的应用。

函数原型

导数的函数原型

适用范围

主要用于二分类的输出层

函数图像

本文介绍高等数学中的tanh函数，以及在神经网络中的应用。

函数原型

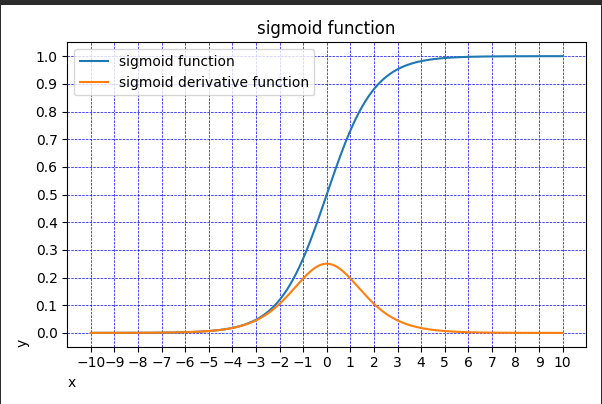
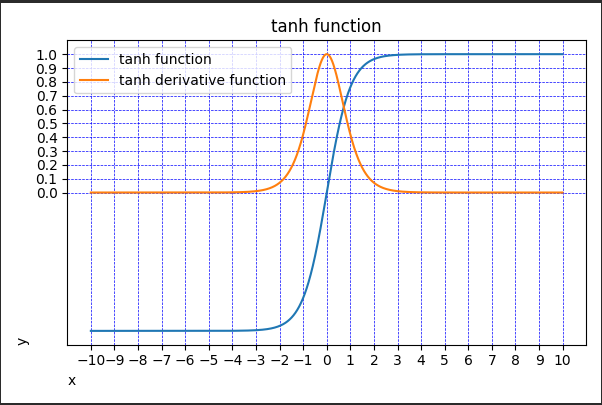
tanh函数又称双曲正切函数

导数的函数原型

适用范围

几乎所有场景

函数图像

本文介绍高等数学中的 e

e介绍

小写字母 "e" 表示自然对数的底（Euler's number），它是一个重要的数学常数。它的值大约是 2.71828。"e" 的名称来自于瑞士数学家莱昂哈德·欧拉（Leonhard Euler），他在18世纪早期对这个数进行了深入的研究。

e的定义

"e" 是一个无限不循环小数，它的值可以用以下级数表示：
   e = 1 + + + + + ...

本文介绍高等数学中的函数求导

求一个函数的导数，即求出该函数的导数表达式，是微积分中的一个基本问题。不同类型的函数有不同的求导规则，以下是一些常见的求导规则：

1. 常数规则：

其中，(c) 是常数。

2. 幂函数规则：

其中，(n) 是常数。